Introduction...

TODO: motivation behind optics

import Optics

and then...

Operators (if you prefer them) are in

import Optics.Operators

This section is work-in-progress

From Adam's talk:

See Talk.pdf, or watch https://skillsmatter.com/skillscasts/10692-through-a-glass-abstractly-lenses-and-the-power-of-abstraction

• optics has an abstract interface: Optic is an opaque type
• Cannot write optics without depending on the package, therefore optics-core doesnt' have non GHC-boot library dependencies. (one cannot write prisms with lens without depending on profunctors, indexed optics require depending on lens ...)

• abstract interface: optics has better error messages (note: silica is a hybrid approach)

  >>> set (to fst)
  ...
  ...A_Getter cannot be used as A_Setter
  ...
  

• abstract interface: better type-inference (optics kind is preserved)

  >>> :t traversed % to not
  traversed % to not
    :: Traversable t => Optic A_Fold '[] (t Bool) (t Bool) Bool Bool
  

• abstract interface: not all optics have Join

  >>> sets map % to not
  ...
  ...A_Setter cannot be composed with A_Getter
  ...
  

• Optic is a Rank1Type (not really before #41), so there are no need for ALens etc.
• Types that say what they mean
• More comprehensible type errors
• Less vulnerable to the monomorphism restriction
• Free choice of lens implementation
• Indexed optics have different interface.

Drawbacks

• Can’t insert points into the subtyping order post hoc

Technical differences

• Composition operator is %
• view is smart
• None of operators is exported from main module
• All ordinary optics are index-preserving by default
• Indexed optics interface is different (let's expand in own section, when the implementation is stabilised)
• There are no Traversal1
• There is AffineTraversal
• We can't use traverse as an optic directly, but there is a Traversal called traversed.
• view is compatible with lens, but it uses a type class which chooses between view1, view01 and viewN (See discussion in GitHub #57: Do we need view at all, and what ^. should be)
• There are no from, only re (Should there be a from restricted to Iso or an alias to re? https://github.com/well-typed/optics/pull/43#discussion_r247121380)

Optics.Optic module provides core definitions:

• Opaque Optic type,
• which is parameterised over a type representing an optic flavour;
• Is and Join relations, illustrated in the graph below;
• and optic composition operators % and %%.

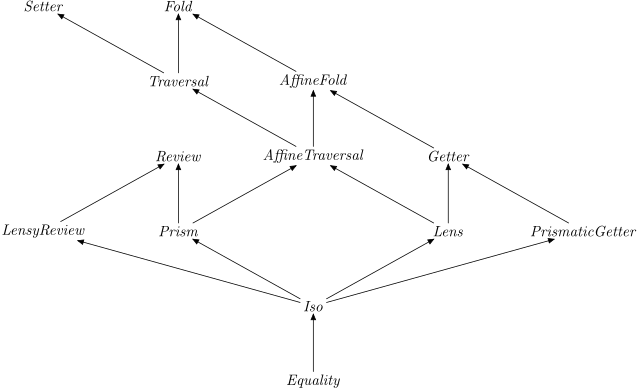
The arrows represent Is relation (partial order). The hierachy is a Join semilattice, for example the Join of a Lens and a Prism is an AffineTraversal.

>>> :kind! Join A_Lens A_Prism
Join A_Lens A_Prism :: Optics.Internal.Optic.Types.OpticKind_ -> *
= An_AffineTraversal

There are also indexed variants of Traversal, Fold and Setter. Indexed optics are explained in more detail in Differences from lens section.

There are 16 (TODO: add modules for LensyReview and PrismaticGetter) different kinds of optics, each documented in a separate module. Each optic module documentation has formation, introduction, elimination, and well-formedness sections.

• The formation sections contain type definitions. For example

  -- Tag for a lens.
  type A_Lens = 'A_Lens
  
  -- Type synonym for a type-modifying lens.
  type Lens s t a b = Optic A_Lens i i s t a b
  

• In the introduction sections are described the ways to construct the particular optic. Continuing with a Lens example:

  -- Build a lens from a getter and a setter.
  lens :: (s -> a) -> (s -> b -> t) :: Lens i s t a b
  

• In the elimination sections are shown how you can destruct the optic into a pieces it was constructed from.

  -- Lens is a Setter and a Getter, therefore you can
  
  view1 :: Lens i s t a b -> s -> a
  set   :: Lens i s t a b -> b -> s -> t
  over  :: Lens i s t a b -> (a -> b) -> s -> t
  

• Computation rules tie introduction and elimination combinators together. These rules are automatically fulfilled.

  view1 (lens f g)   s = f s
  set   (lens f g) a s = g s a
  

• All optics provided by the library are well-formed. Constructing of ill-formed optics is possible, but should be avoided. Ill-formed optic might behave differently from what computation rules specify.

  A Lens should obey three laws, known as GetPut, PutGet and PutPut. See Optics.Lens module for their definitions.

Note: you should also consult the optics hierarchy diagram. Neither introduction or elimination sections list all ways to construct or use particular optic kind. For example you can construct Lens from Iso using sub. Also, as a Lens is also a Traversal, a Fold etc, so you can use traverseOf, preview and many other combinators.

Some optics can be reversed with re: Iso i s t a b into Iso i b a t s, Getter s t a b into Review i b a t s etc. Red arrows illustrate how re transforms optics:

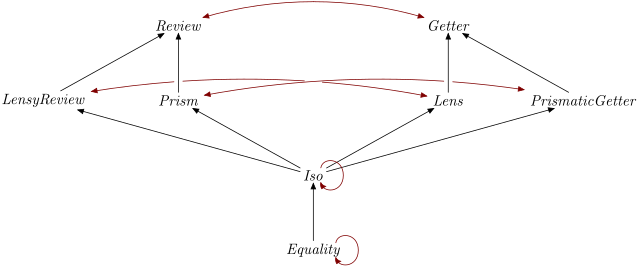
re is mainly useful to invert Isos:

>>> let _Identity = iso runIdentity Identity
>>> view1 (_1 % re _Identity) ('x', "yz")
Identity 'x'

Yet we can use a Lens as a Review too:

>>> review (re _1) ('x', "yz")
'x'

Note: there are no from combinator.

optics library also provides indexed optics, which provide an additional index value in mappings:

over  :: Setter     s t a b -> (a -> b)      -> s -> t
iover :: IxSetter i s t a b -> (i -> a -> b) -> s -> t

Note that there aren't any laws about indices. Especially in compositions same index may occur multiple times.

The machinery builds on indexed variants of Functor, Foldable, and Traversable classes: FunctorWithIndex, FoldableWithIndex and TraversableWithIndex respectively. There are instances for types in the boot libraries.

class (FoldableWithIndex i t, Traversable t)
  => TraversableWithIndex i t | t -> i where
    itraverse :: Applicative f => (i -> a -> f b) -> t a -> f (t b)

Indexed optics can be used as regular ones, i.e. indexed optics gracefully downgrade to regular ones.

>>> toListOf ifolded "foo"
"foo"

But there is also a combinator to explicitly erase indices:

>>> :t ifolded
ifolded :: FoldableWithIndex i f => IxFold i (f a) a

>>> :t unIx ifolded
unIx ifolded
  :: FoldableWithIndex i f => Optic A_Fold '[] (f b) (f b) b b

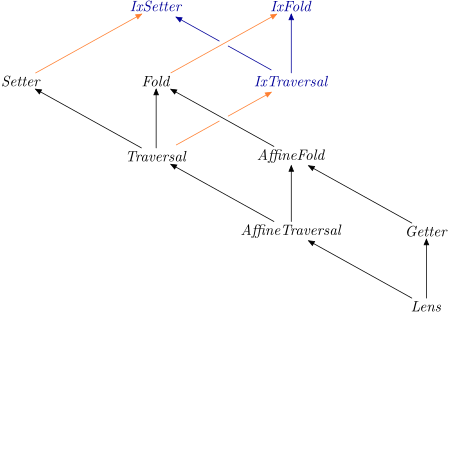
As the example above illustrates (TODO: will do), regular and indexed optics have the same kind, in this case Optic A_Fold. Regular optics simply don't have any indices. The provided type aliases IxFold, IxSetter and IxTraversal are variants with a single index.

In the diagram below, the optics hierachy is amended with these (singly) indexed variants (in blue). Orange arrows mean "can be used as one, assuming it's composed with any optic below the orange arrow first". For example. _1 is not an indexed fold, but itraversed % _1 is, because it's an indexed traversal, so it's also an indexed fold.

>>> let fst' = _1 :: Lens (a, c) (b, c) a b
>>> :t fst' % itraversed
fst' % itraversed
  :: TraversableWithIndex i t =>
     Optic A_Traversal '[i] (t a, c) (t b, c) a b

TODO: write about icompose and multiple indices.

There are yet no IxAffineFold, IxAffineTraversal etc, but they can be added.

A Traversal for a (potentially monomorphic) container.

>>> over each (*10) (1,2,3)
(10,20,30)