All kinds of lattices
This post contains excerpts from a PDF "post" I have written. It looks way better in PDF.
Partial ordered set, or poset for short is well used example in category theory books. Yet, posets are not too familiar for an average CT-curious Haskeller, yet they are easy to visualise! Let’s do exactly that, and mention elementery bits of category theory. In particular, I’ll scan over the six first chapters of Category Theory by Steve Awodey, repeating related definitions and poset examples.1
#Categories
Error:LaTeX failed:
This is pdfTeX, Version 3.141592653-2.6-1.40.22 (TeX Live 2022/dev/Debian) (preloaded format=latex)
restricted \write18 enabled.
entering extended mode
(./working.tex
LaTeX2e <2021-11-15> patch level 1
L3 programming layer <2022-01-21>
(/usr/share/texlive/texmf-dist/tex/latex/extsizes/extarticle.cls
Document Class: extarticle 1996/10/08 v1.0 Non Standard LaTeX document class
(/usr/share/texlive/texmf-dist/tex/latex/extsizes/size14.clo)
(/usr/share/texlive/texmf-dist/tex/latex/base/exscale.sty))
(/usr/share/texmf/tex/latex/preview/preview.sty
(/usr/share/texlive/texmf-dist/tex/generic/luatex85/luatex85.sty)
(/usr/share/texmf/tex/latex/preview/prtightpage.def))
(/usr/share/texlive/texmf-dist/tex/latex/base/fontenc.sty)
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsmath.sty
For additional information on amsmath, use the `?' option.
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amstext.sty
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsgen.sty))
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsbsy.sty)
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsopn.sty))
(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/amssymb.sty
(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/amsfonts.sty))
(/usr/share/texlive/texmf-dist/tex/latex/amscls/amsthm.sty)
(/usr/share/texlive/texmf-dist/tex/latex/stmaryrd/stmaryrd.sty)
(/usr/share/texlive/texmf-dist/tex/latex/psnfss/palatino.sty)
(/usr/share/texlive/texmf-dist/tex/latex/psnfss/mathpazo.sty)
(/usr/share/texlive/texmf-dist/tex/latex/mathtools/mathtools.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/keyval.sty)
(/usr/share/texlive/texmf-dist/tex/latex/tools/calc.sty)
(/usr/share/texlive/texmf-dist/tex/latex/mathtools/mhsetup.sty))
(/usr/share/texlive/texmf-dist/tex/latex/prftree/prftree.sty)
(/usr/share/texlive/texmf-dist/tex/latex/tikz-cd/tikz-cd.sty
(/usr/share/texlive/texmf-dist/tex/latex/pgf/frontendlayer/tikz.sty
(/usr/share/texlive/texmf-dist/tex/latex/pgf/basiclayer/pgf.sty
(/usr/share/texlive/texmf-dist/tex/latex/pgf/utilities/pgfrcs.sty
(/usr/share/texlive/texmf-dist/tex/generic/pgf/utilities/pgfutil-common.tex
(/usr/share/texlive/texmf-dist/tex/generic/pgf/utilities/pgfutil-common-lists.t
ex)) (/usr/share/texlive/texmf-dist/tex/generic/pgf/utilities/pgfutil-latex.def
) (/usr/share/texlive/texmf-dist/tex/generic/pgf/utilities/pgfrcs.code.tex
(/usr/share/texlive/texmf-dist/tex/generic/pgf/pgf.revision.tex)))
(/usr/share/texlive/texmf-dist/tex/latex/pgf/basiclayer/pgfcore.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/graphicx.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/graphics.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/trig.sty)
(/usr/share/texlive/texmf-dist/tex/latex/graphics-cfg/graphics.cfg)
(/usr/share/texlive/texmf-dist/tex/latex/graphics-def/dvips.def)))
(/usr/share/texlive/texmf-dist/tex/latex/pgf/systemlayer/pgfsys.sty
(/usr/share/texlive/texmf-dist/tex/generic/pgf/systemlayer/pgfsys.code.tex
(/usr/share/texlive/texmf-dist/tex/generic/pgf/utilities/pgfkeys.code.tex
(/usr/share/texlive/texmf-dist/tex/generic/pgf/utilities/pgfkeysfiltered.code.t
ex)) (/usr/share/texlive/texmf-dist/tex/generic/pgf/systemlayer/pgf.cfg)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/systemlayer/pgfsys-dvips.def
(/usr/share/texlive/texmf-dist/tex/generic/pgf/systemlayer/pgfsys-common-postsc
ript.def)))
(/usr/share/texlive/texmf-dist/tex/generic/pgf/systemlayer/pgfsyssoftpath.code.
tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/systemlayer/pgfsysprotocol.code.
tex)) (/usr/share/texlive/texmf-dist/tex/latex/xcolor/xcolor.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics-cfg/color.cfg))
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcore.code.tex
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmath.code.tex
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmathcalc.code.tex
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmathutil.code.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmathparser.code.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmathfunctions.code.tex
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmathfunctions.basic.code
.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmathfunctions.trigonomet
ric.code.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmathfunctions.random.cod
e.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmathfunctions.comparison
.code.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmathfunctions.base.code.
tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmathfunctions.round.code
.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmathfunctions.misc.code.
tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmathfunctions.integerari
thmetics.code.tex)))
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmathfloat.code.tex))
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfint.code.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcorepoints.code.te
x)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcorepathconstruct.
code.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcorepathusage.code
.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcorescopes.code.te
x)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcoregraphicstate.c
ode.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcoretransformation
s.code.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcorequick.code.tex
)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcoreobjects.code.t
ex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcorepathprocessing
.code.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcorearrows.code.te
x)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcoreshade.code.tex
)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcoreimage.code.tex
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcoreexternal.code.
tex))
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcorelayers.code.te
x)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcoretransparency.c
ode.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcorepatterns.code.
tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcorerdf.code.tex))
)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/modules/pgfmoduleshapes.code.tex
) (/usr/share/texlive/texmf-dist/tex/generic/pgf/modules/pgfmoduleplot.code.tex
)
(/usr/share/texlive/texmf-dist/tex/latex/pgf/compatibility/pgfcomp-version-0-65
.sty)
(/usr/share/texlive/texmf-dist/tex/latex/pgf/compatibility/pgfcomp-version-1-18
.sty)) (/usr/share/texlive/texmf-dist/tex/latex/pgf/utilities/pgffor.sty
(/usr/share/texlive/texmf-dist/tex/latex/pgf/utilities/pgfkeys.sty
(/usr/share/texlive/texmf-dist/tex/generic/pgf/utilities/pgfkeys.code.tex))
(/usr/share/texlive/texmf-dist/tex/latex/pgf/math/pgfmath.sty
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmath.code.tex))
(/usr/share/texlive/texmf-dist/tex/generic/pgf/utilities/pgffor.code.tex
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmath.code.tex)))
(/usr/share/texlive/texmf-dist/tex/generic/pgf/frontendlayer/tikz/tikz.code.tex
(/usr/share/texlive/texmf-dist/tex/generic/pgf/libraries/pgflibraryplothandlers
.code.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/modules/pgfmodulematrix.code.tex
)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/frontendlayer/tikz/libraries/tik
zlibrarytopaths.code.tex)))
(/usr/share/texlive/texmf-dist/tex/generic/tikz-cd/tikzlibrarycd.code.tex
(/usr/share/texlive/texmf-dist/tex/generic/pgf/frontendlayer/tikz/libraries/tik
zlibrarymatrix.code.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/frontendlayer/tikz/libraries/tik
zlibraryquotes.code.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/libraries/pgflibraryarrows.meta.
code.tex))) (/usr/share/texlive/texmf-dist/tex/latex/psnfss/t1ppl.fd)
(/usr/share/texlive/texmf-dist/tex/latex/l3backend/l3backend-dvips.def)
No file working.aux.
Preview: Fontsize 14.4pt
! LaTeX Error: Environment definition undefined.
See the LaTeX manual or LaTeX Companion for explanation.
Type H <return> for immediate help.
...
l.25 \begin{definition}
[Awodey 1.1]\textbf{Definition} (Awodey 1.1)
(/usr/share/texlive/texmf-dist/tex/latex/psnfss/ts1ppl.fd)
(/usr/share/texlive/texmf-dist/tex/latex/psnfss/ot1ppl.fd)
(/usr/share/texlive/texmf-dist/tex/latex/psnfss/omlzplm.fd)
(/usr/share/texlive/texmf-dist/tex/latex/psnfss/omszplm.fd)
(/usr/share/texlive/texmf-dist/tex/latex/psnfss/omxzplm.fd)
(/usr/share/texlive/texmf-dist/tex/latex/stmaryrd/Ustmry.fd)
(/usr/share/texlive/texmf-dist/tex/latex/psnfss/ot1zplm.fd)
! LaTeX Error: \begin{preview} on input line 24 ended by \end{definition}.
See the LaTeX manual or LaTeX Companion for explanation.
Type H <return> for immediate help.
...
l.64 \end{definition}
Preview: Tightpage -32891 -32891 32891 32891
[1] (./working.aux) )
(see the transcript file for additional information)
Output written on working.dvi (1 page, 12380 bytes).
Transcript written on working.log.
We’ll see how Category type-class is related later, in later section.
…
#Functor
Before proceeding, we’ll answer a question: is there a category with posets as objects? Yes, it’s called ! What are the arrows in this category? An arrow from a poset to a poset is a function
that is monotone, in the sense that, for all ,
We need to know that is monotone, and also that if and are monotone, then is monotone. That holds, check!
Recall, posets are categories, so monotone functions are "mappings" between categories. A "homomorphism2 of categories" is called a functor.
Error:LaTeX failed:
This is pdfTeX, Version 3.141592653-2.6-1.40.22 (TeX Live 2022/dev/Debian) (preloaded format=latex)
restricted \write18 enabled.
entering extended mode
(./working.tex
LaTeX2e <2021-11-15> patch level 1
L3 programming layer <2022-01-21>
(/usr/share/texlive/texmf-dist/tex/latex/extsizes/extarticle.cls
Document Class: extarticle 1996/10/08 v1.0 Non Standard LaTeX document class
(/usr/share/texlive/texmf-dist/tex/latex/extsizes/size14.clo)
(/usr/share/texlive/texmf-dist/tex/latex/base/exscale.sty))
(/usr/share/texmf/tex/latex/preview/preview.sty
(/usr/share/texlive/texmf-dist/tex/generic/luatex85/luatex85.sty)
(/usr/share/texmf/tex/latex/preview/prtightpage.def))
(/usr/share/texlive/texmf-dist/tex/latex/base/fontenc.sty)
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsmath.sty
For additional information on amsmath, use the `?' option.
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amstext.sty
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsgen.sty))
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsbsy.sty)
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsopn.sty))
(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/amssymb.sty
(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/amsfonts.sty))
(/usr/share/texlive/texmf-dist/tex/latex/amscls/amsthm.sty)
(/usr/share/texlive/texmf-dist/tex/latex/stmaryrd/stmaryrd.sty)
(/usr/share/texlive/texmf-dist/tex/latex/psnfss/palatino.sty)
(/usr/share/texlive/texmf-dist/tex/latex/psnfss/mathpazo.sty)
(/usr/share/texlive/texmf-dist/tex/latex/mathtools/mathtools.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/keyval.sty)
(/usr/share/texlive/texmf-dist/tex/latex/tools/calc.sty)
(/usr/share/texlive/texmf-dist/tex/latex/mathtools/mhsetup.sty))
(/usr/share/texlive/texmf-dist/tex/latex/prftree/prftree.sty)
(/usr/share/texlive/texmf-dist/tex/latex/tikz-cd/tikz-cd.sty
(/usr/share/texlive/texmf-dist/tex/latex/pgf/frontendlayer/tikz.sty
(/usr/share/texlive/texmf-dist/tex/latex/pgf/basiclayer/pgf.sty
(/usr/share/texlive/texmf-dist/tex/latex/pgf/utilities/pgfrcs.sty
(/usr/share/texlive/texmf-dist/tex/generic/pgf/utilities/pgfutil-common.tex
(/usr/share/texlive/texmf-dist/tex/generic/pgf/utilities/pgfutil-common-lists.t
ex)) (/usr/share/texlive/texmf-dist/tex/generic/pgf/utilities/pgfutil-latex.def
) (/usr/share/texlive/texmf-dist/tex/generic/pgf/utilities/pgfrcs.code.tex
(/usr/share/texlive/texmf-dist/tex/generic/pgf/pgf.revision.tex)))
(/usr/share/texlive/texmf-dist/tex/latex/pgf/basiclayer/pgfcore.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/graphicx.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/graphics.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/trig.sty)
(/usr/share/texlive/texmf-dist/tex/latex/graphics-cfg/graphics.cfg)
(/usr/share/texlive/texmf-dist/tex/latex/graphics-def/dvips.def)))
(/usr/share/texlive/texmf-dist/tex/latex/pgf/systemlayer/pgfsys.sty
(/usr/share/texlive/texmf-dist/tex/generic/pgf/systemlayer/pgfsys.code.tex
(/usr/share/texlive/texmf-dist/tex/generic/pgf/utilities/pgfkeys.code.tex
(/usr/share/texlive/texmf-dist/tex/generic/pgf/utilities/pgfkeysfiltered.code.t
ex)) (/usr/share/texlive/texmf-dist/tex/generic/pgf/systemlayer/pgf.cfg)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/systemlayer/pgfsys-dvips.def
(/usr/share/texlive/texmf-dist/tex/generic/pgf/systemlayer/pgfsys-common-postsc
ript.def)))
(/usr/share/texlive/texmf-dist/tex/generic/pgf/systemlayer/pgfsyssoftpath.code.
tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/systemlayer/pgfsysprotocol.code.
tex)) (/usr/share/texlive/texmf-dist/tex/latex/xcolor/xcolor.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics-cfg/color.cfg))
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcore.code.tex
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmath.code.tex
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmathcalc.code.tex
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmathutil.code.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmathparser.code.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmathfunctions.code.tex
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmathfunctions.basic.code
.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmathfunctions.trigonomet
ric.code.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmathfunctions.random.cod
e.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmathfunctions.comparison
.code.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmathfunctions.base.code.
tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmathfunctions.round.code
.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmathfunctions.misc.code.
tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmathfunctions.integerari
thmetics.code.tex)))
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmathfloat.code.tex))
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfint.code.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcorepoints.code.te
x)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcorepathconstruct.
code.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcorepathusage.code
.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcorescopes.code.te
x)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcoregraphicstate.c
ode.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcoretransformation
s.code.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcorequick.code.tex
)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcoreobjects.code.t
ex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcorepathprocessing
.code.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcorearrows.code.te
x)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcoreshade.code.tex
)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcoreimage.code.tex
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcoreexternal.code.
tex))
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcorelayers.code.te
x)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcoretransparency.c
ode.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcorepatterns.code.
tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/basiclayer/pgfcorerdf.code.tex))
)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/modules/pgfmoduleshapes.code.tex
) (/usr/share/texlive/texmf-dist/tex/generic/pgf/modules/pgfmoduleplot.code.tex
)
(/usr/share/texlive/texmf-dist/tex/latex/pgf/compatibility/pgfcomp-version-0-65
.sty)
(/usr/share/texlive/texmf-dist/tex/latex/pgf/compatibility/pgfcomp-version-1-18
.sty)) (/usr/share/texlive/texmf-dist/tex/latex/pgf/utilities/pgffor.sty
(/usr/share/texlive/texmf-dist/tex/latex/pgf/utilities/pgfkeys.sty
(/usr/share/texlive/texmf-dist/tex/generic/pgf/utilities/pgfkeys.code.tex))
(/usr/share/texlive/texmf-dist/tex/latex/pgf/math/pgfmath.sty
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmath.code.tex))
(/usr/share/texlive/texmf-dist/tex/generic/pgf/utilities/pgffor.code.tex
(/usr/share/texlive/texmf-dist/tex/generic/pgf/math/pgfmath.code.tex)))
(/usr/share/texlive/texmf-dist/tex/generic/pgf/frontendlayer/tikz/tikz.code.tex
(/usr/share/texlive/texmf-dist/tex/generic/pgf/libraries/pgflibraryplothandlers
.code.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/modules/pgfmodulematrix.code.tex
)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/frontendlayer/tikz/libraries/tik
zlibrarytopaths.code.tex)))
(/usr/share/texlive/texmf-dist/tex/generic/tikz-cd/tikzlibrarycd.code.tex
(/usr/share/texlive/texmf-dist/tex/generic/pgf/frontendlayer/tikz/libraries/tik
zlibrarymatrix.code.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/frontendlayer/tikz/libraries/tik
zlibraryquotes.code.tex)
(/usr/share/texlive/texmf-dist/tex/generic/pgf/libraries/pgflibraryarrows.meta.
code.tex))) (/usr/share/texlive/texmf-dist/tex/latex/psnfss/t1ppl.fd)
(/usr/share/texlive/texmf-dist/tex/latex/l3backend/l3backend-dvips.def)
No file working.aux.
Preview: Fontsize 14.4pt
! LaTeX Error: Environment definition undefined.
See the LaTeX manual or LaTeX Companion for explanation.
Type H <return> for immediate help.
...
l.25 \begin{definition}
[Awodey 1.2]\textbf{Definition} (Awodey 1.2)
(/usr/share/texlive/texmf-dist/tex/latex/psnfss/ot1ppl.fd)
(/usr/share/texlive/texmf-dist/tex/latex/psnfss/omlzplm.fd)
(/usr/share/texlive/texmf-dist/tex/latex/psnfss/omszplm.fd)
(/usr/share/texlive/texmf-dist/tex/latex/psnfss/omxzplm.fd)
(/usr/share/texlive/texmf-dist/tex/latex/stmaryrd/Ustmry.fd)
(/usr/share/texlive/texmf-dist/tex/latex/psnfss/ot1zplm.fd)
(/usr/share/texlive/texmf-dist/tex/latex/psnfss/ts1ppl.fd)
! LaTeX Error: \begin{preview} on input line 24 ended by \end{definition}.
See the LaTeX manual or LaTeX Companion for explanation.
Type H <return> for immediate help.
...
l.40 \end{definition}
Preview: Tightpage -32891 -32891 32891 32891
[1] (./working.aux) )
(see the transcript file for additional information)
Output written on working.dvi (1 page, 11660 bytes).
Transcript written on working.log.
The version looks quite different:
class Functor f where
fmap :: (a -> b) -> f a -> f bThere is a mismatch of a notation of category theory, and what can be written as code. In CT notation acts both on objects and arrows. In f acts on objects, and fmap f acts on arrows. Substituting above, id and . into definition of functor, will also give familiar laws
fmap id = id
fmap (g . f) = fmap g . fmap fHowever, Functor-class is only for functors from a pseudo-category to itself, where f, a mapping from types to types is a type-constructor, not arbitrary type family. Functor is a very special case of category theoretical variant.
With small posets, like Bool and M2 we can visualise a monotone function, a functor. Let’s consider a function
f :: Bool -> M2
f True = M2i
f False = M2o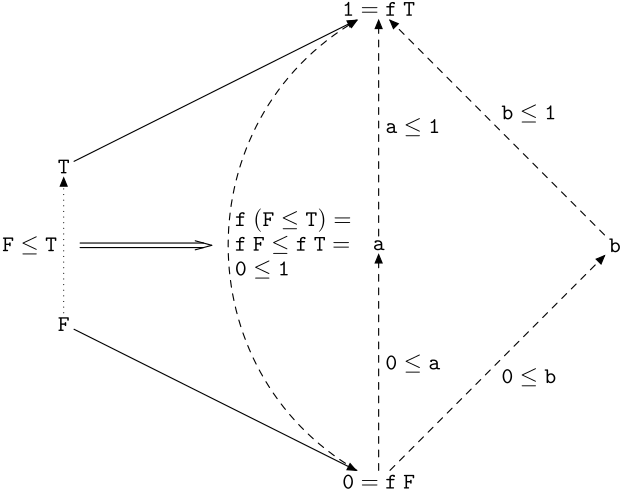
f :: Bool -> M2The graph of f is on . Dotted and dashed lines are arrows in Bool and M2 respectively. We can see on figure, that f indeed gives a picture of Bool in M2.
In we have only written a mapping of objects, True and False. The mapping of arrows is something we need to check, to be able to claim that f is a functor, and therefore a monotone function. The other way around, there are mappings from Bool to M2 which aren’t monotone, and aren’t functors.
In this section we went backwards. More principal approach would been to first consider functors between poset categories. The monotonicity requirement is implied by first functor requirement. This is a power of category theory. When you look for something, category theory tells you which properties it should have. Once you find something which satisfies the requirements, you know that it’s the right one (up to an isomorphism).
…
Exponential lattices with M2 are pretty. ZHO -> M2 () has nice planar graph. . Yet the final stress test is (ZHO -> ZHO) -> ZHO, or is on . A beautiful monster.
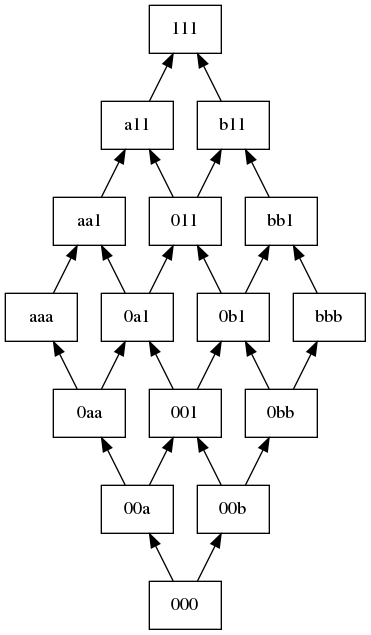
ZHO -> M2 lattice
(ZHO -> ZHO) -> ZHO lattice- 2025-02-13 – PHOAS to de Bruijn conversion
- 2025-02-11 – NbE PHOAS
- 2024-06-24 – hashable arch native
- 2024-05-28 – cabal fields
- 2024-04-21 – A note about coercions
 This work is licensed under a “CC BY SA 4.0” license.
This work is licensed under a “CC BY SA 4.0” license.