Oleg's gists — Archive

Regular expression of types

Posted on 2018-09-13 by Oleg Grenrus

This is a script of the talk I gave at Small FP 2018. There is a video recording of the talk and the slide deck as a PDF.

This work is licensed under a “CC BY SA 4.0” license.

#Introduction

#Me

My name is Oleg. In online communities (Twitter, GitHub, IRC ...) I use nick as on the slide. I prefer that it's pronounced as "Oleg".

I work at the futurice, which is an IT-consultancy. I don't work with clients, but write internal software, in Haskell.

I'm also one of the organisers of HaskHEL - Helsinki Haskell User Group meetup.

And finally, I'm a release manager (whatever that means) of servant Haskell web-framework (or library?). It's know for its type-level stuff. This talk is also about type-level stuff.

But first: we need to find a problem to solve.

#Find

I hope all of you are familiar with the find utility. If you lookup it's documentation, there's a synopsis which looks like that.

Shell programming - stringly typed programming at extreme. Command are strings, Arguments are strings, Inputs and outputs are also strings.

What is we had a little more structure in the language...

... would you write a function with a spec like that? For you who don't know, it's a clojure.spec definition of arguments of imaginary thin wrapper around find - the shell utility.

#Using find

Let's see find from a different perspective.

In shell, we'll pass a list of strings to the find command. Its internal arguments parser will verify that we didn't make a mistake, and then the find will do its job.

In Clojure, situation is quite similar. With clojure.spec we can check that arguments conform to the spec. We have richer primitives (not only strings, but also keywords and so on), and a uniform approacch speccing. The check is still dynamic.

But in GHC Haskell, we could also look very dynamic; yet perform the checks statically! Syntax (almost) like LISP, but with static types. What could be better?

So let me describe how we can have regular expressions of types.

#Types

Let me start with a very little of type theory.

#Lambda calculus

Type systems are described using a rules like one on the slide. Red parts are programs, and blue parts are types of those programs. Rules tie it all together in a very concise notation. As it probably not familiar, let me explain it; so after this talk you can go out and read all type theory related literature with ease.

Rules have a names, so we can talk about them. The part below the line is the conclusion, the part above are premises. We can then combine rules into trees, where conclusion of the first rule is the premise of the second rules. We'll see an example of that later.

Gamma (or some other Greek capital letter) denote a context. It abreviates a thing we know already. For example it could be there is an x of type Int and y of type Bool in the context.

The turnstile symbol is just a symbol.

Single colon is usually used to denote has type. Haskell uses double colon though.

So we can read the rule out loud.

The fancy notation pays off. It's more concise and visual.

#Lambda calculus: more rules

And of course there are more rules.

The rule for use of variables is on the top. If there is a variable in scope, we can use it. And so on...

#Decidability of lambda calculi

When we have a type-system, we can ask some questions about it. There are three typical questions one could ask.

Is the type checking decidable. In other words if you give me a program x and claim it's type is alpha, can it verify that? Is there an algorithm to get a yes or no answer.

That is a minimum you would expect from a type-system. Surpisingly or not, that's not true for many type systems in use, either the compiler can be sent into the loop, or it rejects some programs it shouldn't.

Second question is about type-inference. Look here I have a program x, can you tell what type it has? The problem can easily made decidable by requiring a lot of type-annotations for program to be even syntactically valid. Yet, we are humans so we like convinience. We don't want to write too much type annotations. So some type inference is a MUST requirement nowadays.

The holy grail is the inhabitation. I have this type (or should I say specification). Computer, give me a program with this type. Obviously that's not as easy. Either the types are not expressive enough, so there are too many programs with needed type, and most of them are not the ones we want. Or then the inhabitation is simply undecidable, so we need a human to find an answer.

#Inhabitation, an example

The system above is Simply typed lambda calculus. I promised you to show a derivation tree, so here it goes.

Let's try to find a term which has the type above. It's a type of a curry function.

The type we want is a function type. So we can use Lam-rule to simplify a problem. Context was empty, but now we have a function f there.

Then we can apply Lam rule two times more. Here I use Γ to abbreviate the context, which has f, x and y. Now we need find a way to make a term of type C.

Next we need to make a right guess for what to use from the context. It's not x and it's not y, as they have wrong types. The only thing left is function f. And there's only way to use a function, apply some argument to it.

So next we need to construct a pair A × B. There's a rule for that.

We have a term of type A in the context...

as well as the term of type B.

Now we are done.

What I showed you, is a typed-hole driven development. There are holes, and we try to fill them with terms of right types. For this example machine could have done it. Machine is very good in finding boring programs. For example if you ask it for a list, it will always propose an empty list first.

Now we have seen enough of types. Let's go to the next part: regular expressions.

#Regular expressions

#Stand back

... as some might have seen in computer science classes. Finite automata and so on.

So regular expression may be

  • empty
  • just a character from an alphabet, note that character doesn't need to be a character. We will have types as characters.
  • We can concatenate regular expressions
  • Or union them
  • Or take Kleene closure of it. zero or many occurences.

Kleene closure is what makes regular expressions interestring.

#Matching

We all probably have some intuition of Does this regular expression matches that string?

We can formalise that intuition precisely.

For me it's not enough if the answer is yes or no. Please give me some evidence backing that Boolean claim.

To write down evidence, we need rules. Concat rule is quite simple. What does r1 <> r2 matches?

It depends on what r1 matches.

Let's say it matches some ∆1.

Similarly, if r2 matches some ∆2, then...

r1 <> r2 matches ∆1 ++ ∆2.

Matches our intuition, and n ow we have formal rule to use.

#And there are more rules

And there are more rules. Empty string matches empty list; Alternative matches if either left or right part matches. Kleene star can match an empty list, or one time followed by a recursive match.

#A match

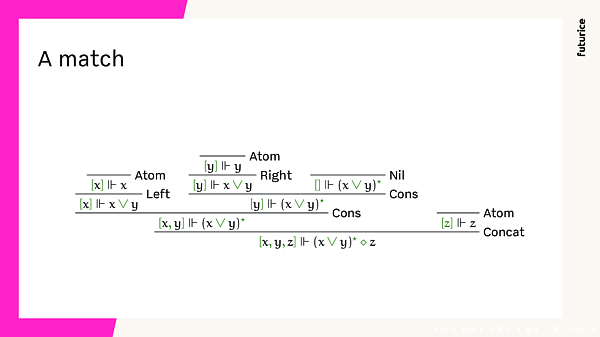
We can return to the [x,y,z] ||- (x \/ y)* <> z match. Now we have means to write a match proof (actual proof object is omitted though).

#REList

You might have noticed some similarities.

What we can do, is ditch pairs, and use lists. Indexed by regular expressions.

We'll only need REList, no pairs, not either, no ordinary lists. Just single REList to rule them all.

#What's the point?

A very natural question you might ask is, what's the point? The programs look exactly as before, but the types are way more complex. Why I am torturing you with this?

Well, the point is that we can have another prettier syntax. After all, REList is a list!

#Does it work?

Suspicisious should you be.

This thing is possible, and it works.

Regular expressions are so simple, that the matching relation is decidable. In other words we can ask a computer whether there is a match.

In fact, with my plugin, we can ask GHC, the Glasgow Haskell compiler.

#find - again

As a refreshed, find again. We can rewrite a clojure.spec regexp in a fancy mathematical notation.

#Let's put regular expressions into types

Then we can work with the fancy type.

And translate it to Haskell.

And use that synonym to give a type to the find_ function, I showed in the very beginning of the talk.

It's ok to not believe me now. This all is just fancy symbols on slides. Let me show you that it's real.

#Demo

The code for the library is on GitHub: github.com/phadej/kleene-type.

#Syntax

First, some syntax. This is made possible in GHC-8.6 with source plugins. Double square brackets construct heterogenous lists, lists where elements may have different types.

heterogenousList = [[ True, 'x', "SmallFP" ]]
λ> :t heterogenousList 
heterogenousList :: HList '[Bool, Char, [Char]]

λ> heterogenousList 
True ::: 'x' ::: "SmallFP" ::: Nil

The mix parentheses + square brackets is a syntax for REList. We need to supply a type, otherwise system doesn't know which regexp we want. Here the type-checker plugin kicks in, and verifies that list matches the regexp.

exampleRelist = ([ True, 't', False, 'f' ]) :: REList (S (V Bool <> V Char))
λ> :t exampleRelist 
exampleRelist :: REList (S (V Bool <> V Char))
λ> exampleRelist 
REList (matchC ...) (True ::: 't' ::: False ::: 'f' ::: Nil)

And finally the double parentheses

exampleCall = (( find_, #type, #f, "plugin", "src" ))

It does works:

λ *Main> exampleCall 
>>> find plugin src -type f
plugin/KleenePlugin/TypeEq.hs
plugin/KleenePlugin/Matching.hs
plugin/KleenePlugin/Names.hs
plugin/KleenePlugin/Types.hs
plugin/KleenePlugin/Elaborate.hs
plugin/KleenePlugin/SWT.hs
plugin/KleenePlugin/Debug.hs
plugin/KleenePlugin/SourcePlugin.hs
plugin/KleenePlugin/Synthesis.hs
plugin/KleenePlugin/TcPlugin.hs
plugin/KleenePlugin.hs
src/Kleene/.Type.hs.swp
src/Kleene/Type.hs
src/Kleene/Type/Examples.hs
src/Kleene/Type/Examples/KleeneSH.hs

#Error cases

I implemented some error reporting, it's not just "you are wrong".

findError = (( find_, #type, #b, "plugin", "src" ))
test/KleeneDemo.hs:27:13: error:
    • Regular expression doesn't match, unexpected x0
    • Regular expression
        list
          (FilePath \/
           Key "name" <> FilePath \/
           Key "type" <> (Key "d" \/ Key "f"))
    • Type list [x0, x0, [Char], [Char]]
    • In a matching state
        (Key "d" \/ Key "f") <>
        list
          (FilePath \/
           Key "name" <> FilePath \/
           Key "type" <> (Key "d" \/ Key "f"))
    • Unexpected ‘x0’ followed by [[Char], [Char]]
    • Expecting Key "d", Key "f"
   |
27 | findError = (( find_, #type, #b, "plugin", "src" ))
   |

#Unions

Unions is one thing where this starts to look fancy:

charOrBool :: REList (V Char \/ V Bool) -> IO ()
charOrBool re = withREList re $ withUnion
    (withV print)
    (withV (print . not))
ex1 = (( charOrBool, 'a' ))
ex2 = (( charOrBool, True ))
λ> ex1
'a'
λ> ex2
False

And it doesn't allow "anything" possible:

err1 = (( charOrBool, "foobar" ))
test/KleeneDemo.hs:41:8: error:
    • Regular expression doesn't match, unexpected [Char]
    • Regular expression Char \/ Bool
    • Type list [[Char]]
    • In a matching state Char \/ Bool
    • Unexpected ‘[Char]’ followed by []
    • Expecting Char, Bool
   |
41 | err1 = (( charOrBool, "foobar" ))
   |

#Top - anything

There is also matches anything regular expression: called top.

For example singleBool, accepts anything, as far as there's exactly one Bool.

singleBool :: REList (T <> V Bool <> T) -> Bool
singleBool re = withREList re $ withAppend3 (\_ x _ -> x)
    (withTop ())
    (withV id)
    (withTop ())
ex3 = (( singleBool, 'a', 'b', 'c', True, 'x', "foo", Left 'l' ))
λ> ex3
True

#Haskelly

Last thing is Haskelly type level function. It converts the regular expression to "normal" Haskell type, which would represent he match

λ> :kind! Haskelly (T <> V Bool <> T)
Haskelly (T <> V Bool <> T) :: *
= (Int, (Bool, Int))

It makes writing functions working on REList more convinient in some cases:

singleBool' :: REList (T  <> V Bool <> T) -> Bool
singleBool' (REList m xs) = case haskelly m xs of
    (_, (b, _)) -> b
ex4 = (( singleBool, False ))
λ> ex4
False

#Talk conclusion

I hope you agree.

I still prefer the "normal" Haskell style.

Further work would be to include the rule Sub. This would allow to drop REList, in other world, really get a best of both world: concise expression syntax, but keep Haskell types... without any quirks. It's not super-difficult problem, but requires some engineering time.

#Thank you! Questions?

  • Can you do this for Context-Free Grammars? In theory probably, but there are no concise way to write these grammars "inline" for the types. Futhermore, I don't know how the evidence values will look like.

#References & pointers

One can read more about regular-expressions from

The regular-expressions as types interpretaiton seems to result into Non-commutative linear logic (with lists).

#ImageMagick

Mainly for myself: this is how I made per-slide images.

convert -density 300 -filter Catrom -distort Resize '600x' slides.pdf regex-of-types-%02d.png
pngquant regex-of-types-*
This work is licensed under a “CC BY SA 4.0” license.
Oleg's gists — Archive

twitter github email linkedin stackoverflow

Site proudly generated by Hakyll