Should fmap coerce = coerce hold?

Discussion around (limitations of) Coercible, GeneralizedNewtypeDeriving or DerivingVia resume once in a while.

One common question is whether fmap coerce = coerce should be a law of the Functor type-class, or not. Intuitively, it's similar to the identity law: fmap id = id law, but intuition is not good enough reason alone.

#Category theory may say...

The identity law comes from category theory, so what could category theory say about fmap coerce = coerce like proposition?

Let us consider an endofunctor from a three element category to itself, which "rotates the category".

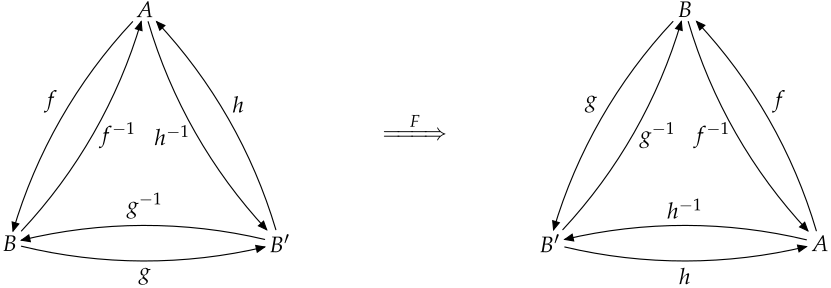
maps objects to respectively. Careful reader would ask how maps morphisms. See an appendix, for a justification.

To make it more concrete we can think that as:

type A     = Int
type B     = Word
newtype B' = B' Word

with isomorphisms in between (assuming Int and Word have the same amount of bits).

Then, we know that Coercible B B'. And arrows and on the diagram are coerce @B @B' and coerce @B' @B. But Coercible (F B) (F B') = Coercible B' A doesn't exist. is a function like \(B' w) -> fromIntegral w which is not coerce.

The functor doesn't preserve the Coercible relation, even it's a categorically lawful functor.

#... but ...

But the functor above is not a Functor as in Haskell. Not even if we try to define

data F :: Type -> Type where
   FA  :: A  -> F A
   FB  :: B  -> F B
   FB' :: B' -> F B'

we'll not be able to write fmap :: (a -> b) -> F a -> F b, as b can be anything, not only A, B or B'.

fmap is polymorphically parametric. There are papers and blogs explaining parametricity¹.

The key insight of parametricity is that we can read types as relations. For example a list defined as

data List x = Nil | Cons x (List x)

can be read as a relation constructor:

Given a relation R :: Relation X Y, xs :: List X and ys :: List Y are related with List R :: Relation (List X) (List Y), if either

• xs = Nil and ys = Nil, or
• xs = Cons x xs', ys = Cons y ys', and x and y are related by R, and xs' and ys' are recursively related by List R.

In other words, List R relates lists of equal length, when all elements are related pointwise.

We can derive free theorems for polymorphic functions over lists, or ...

We could take R X Y to be Coercible X Y. Relation doesn't need to be functional. Coercible is a binary-relation. We can reason that List Coercible is Coercible for lists: Lists related by coerce @(List X) @(List Y) are of the same length and each element is related by coerce @X @Y.

#Functor should be parametric!

Maybe instead of asking whether fmap coerce = coerce should be a law of the Functor type-class, we should ask whether Functor should be a type-class of parametric type constructors? Parametricity would imply fmap coerce = coerce. Non-requirement of parametricity, would mean that opaque types can be "lawfully" Functor, e.g. similarly as Set a has an Eq instance.

The latter choice allows us to write type internally used in the bifunctors library:

data Mag a b t where
    Pure  :: t -> Mag a b t
    Map   :: (x -> t) -> Mag a b x -> Mag a b t
    Ap    :: Mag a b (t -> u) -> Mag a b t -> Mag a b u
    One   :: a -> Mag a b b

instance Functor (Mag a b) where
    fmap  = Map

instance Applicative (Mag a b) where
    pure  = Pure
    (<*>) = Ap

Mag is not lawful Functor, it violates fmap id = id property. but is used to implement traverseBiaWith.

However, there is a comment in the code:

-- Note: if it's necessary for some reason, we *could* relax GADTs to
-- `ExistentialQuantification` by changing the type of One to
-- 
--     One :: (b -> c) -> a -> Mag a b c

Then Mag will be Coercible in all argument, current Mag has type role Mag representational nominal nominal.

A third alternative is to use

One :: Coercible b c => a -> Mag a b c

GHC is smart enough to infer that this Mag variant is also representational in all arguments. Unfortunately, to implement traverseBiaWith, we'll need to change the required constraints

-  Biapplicative p
+( Biapplicative p
+, forall u v x y. (Coercible u x, Coercible v y)
+                => Coercible (p u v) (p x y))
+)

... or require Bifunctor (a superclass of Biapplicative) to be parametric in its both arguments!

For me, it looks like that the addition of (forall x y. Coercible x y => Coercible (f x) (f y)) constraint to Functor (and similarly for Bifunctor, Profunctor, Contravariant ...) can be worked around in all cases. The Mag is the only example mentioned as useful but not lawful Functor, ² and we have demonstrated a required change.

Note: Mag will still be unlawful, but it can be made representational in all arguments. In the implementation of traverseBiaWith we will use coerce which is free operationally, so there shouldn't be any performance degradation.

I cannot come up with an example of f :: Type -> Type which would violate fmap id = id law, but obey fmap coerce = coerce one (or an opposite direction). And I cannot show that fmap coerce = coerce follows from other two Functor laws, but without using parametricity. Edward Kmett explains how Functor composition law follows from identity law and parametricity. Coerce law is implied by parametricity directly.

#Conclusion

Finally, my conclusion is that both

• fmap coerce = coerce should be a law of GHC Haskell Functor, and
• the forall a b. Coercible a b => Coercible (f a) (f b) be Functor super-constraint

even the change departs us far far from Haskell2010. The justification is that these requirements are implied by parametricity, and Functor class should contain only parametric type constructors. We would still be able to have unlawful Functors if really needed.

Some immediate benefits are ability to put join into Monad or that van Laarhoven Lens s t a b would be representable in all arguments.

The disadvantage is that there's Haskell 2010 code which would be broken by that change. Consider

data Eq a => Foo a

We can write (unlawful) Functor instance in Haskell 2010, which won't be accepted, as Foo role is nominal. Yet, GHC documentation about DatatypeContexts says This is widely considered a misfeature, and is going to be removed from the language. You need to enable a language feature to write Foo, in other words that code is already broken (since November 2010!)

Also a non-Haskell2010 code will be broken:

type family Id (x :: Type) :: Type where
  Id x = x

newtype I x = I (Id x)

You may think, there's an easy solution, but there is a five year old issue about roles for type families. Also it have to be investigated, if someone actually wrote an (unlawful) Functor wrapping a type family which pattern matches (i.e. is non-parametric) on an argument, and why they did that!

Just adding fmap coerce = coerce law wouldn't break any code. Something which is unlawful will be a bit more unlawful. The hypothesis is that fmap coerce = coerce won't make any currently lawful Functors into unlawful one.

#Acknowledgments

I'm thankful to Ryan Scott for many discussions and valuable insights. And to Andres Löh for comments on a draft of this post.

#Appendix: Mapping of morphisms

In this category there is an unique arrow between any two objects, so the mapping is trivial.

We can extend the category by adding more objects and morphisms, and so it keeps all other objects in place. In this case mapping of morphisms is trickier. If we require that and others identities suggested by names or arrows we can make it work.

Let us define two families of morphisms indexed by objects in : and

Using these, we can define mapping of morphisms as

For example is mapped to

Check by looking at the diagram!

The identity and composition properties hold, for example

• 2025-02-13 – PHOAS to de Bruijn conversion
• 2025-02-11 – NbE PHOAS
• 2024-06-24 – hashable arch native
• 2024-05-28 – cabal fields
• 2024-04-21 – A note about coercions

twitter github email linkedin stackoverflow