ANN: topograph

I'm happy to announce a new package: topograph. I says in its description:

Directed acyclic graphs can be sorted topographically. Existence of topographic ordering allows writing many graph algorithms efficiently. And many graphs, e.g. most dependency graphs are acyclic!

There are some algorithms build-in: dfs, transpose, transitive closure, transitive reduction... Some algorithms even become not-so-hard to implement, like a longest path!

Directed acyclic graphs are, as the name says, graphs without cycles. Such graphs are common in dependency management. In fact, my first use case was to analyse Haskell package dependencies.

Because there are no cycles, many graph-problems are much easier to solve than their general versions. A property is that graph can be topologically ordered; i.e. there is a linear ordering of its vertices, such that... (wikipedia). Or more concretely, we can assign each vertex an index, such that if i > j, there aren't path from i to j.

The running example graph will be

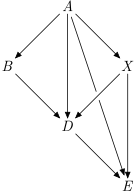
It's a DAG. We can order vertices ABXDE (or AXBDE, check that both are valid topological orderings!). I marked one node X to make it clearer, that you don't need to label nodes in the topological ordering :)

• Is there a path from E to D? No. 4 > 3.
• Is there a path from B to X? If we use ABXDE as the ordering, we know that maybe, we need to look closer.

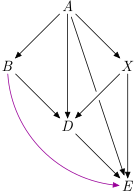
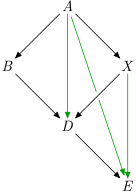
topograph have few algorithms built-in, e.g. transitive closure (added purple edge) and transitive reduction (green edges removed). Curiously, they are implemented using the same function parameterised by different predicate. Take a look at the source.

The library uses runST-method to hide the fact that indices are actually Ints, by requiring that algorithms are written over universal i. For example the type of transitive closure is

closure :: Ord i => G v i -> G v i

At the end, you can run algorithms with the runG function:

runG
    :: forall v r. Ord v
    => Map v (Set v)
       -- ^ Adjacency Map
    -> (forall i. Ord i => G v i -> r)
       -- ^ function on linear indices
    -> Either [v] r                    
       -- ^ Return the result or a cycle in the graph.

You pass in an adjacency map representation, an algorithm and you get either a Right result, or a Left if there were a cycle.

In a discussion on Twitter, Andrey Mokhov mentioned that there is a Summer of Haskell idea to add type-safe representation for acyclic graphs to alga. When it gets implemented, we can add a variant of runG which always succeeds!

Finally, I want to show a small, but real example where I used topograph. That hopefully illustrates how relatively easy is to do stuff with topograph.

stuff adjMap = either (fail . show) id $ runG adjMap $ \g -> do
    -- take a closure and bring all the fields of G in scope        
    let G {..} = closure g

    -- double loop
    for_ gVertices $ \a -> for_ gVertices $ \b -> when (a < b) $ do
        -- edge destinations
        let ae = Set.fromList $ gEdges a
        let be = Set.fromList $ gEdges b

        -- an exercise: what is cs?
        let cs | a `elem` be = [a]
               | b `elem` ae = [b]
               -- Here we are clever,
               -- Set.minView and no foldr would be ok for some graphs
               -- Why?
               | otherwise = case Set.maxView $ Set.intersection ae be of
                   Nothing      -> []
                   Just (x, xs) -> foldr f [x] xs where
                       f y zs = y : filter (`notElem` gEdges y) zs

        -- print results
        -- in real version this part is fancier
        print (gFromVertex a, gFromVertex b, map gFromVertex cs)

An exercise is to find out what does stuff do. Hint: I give a result of running it with an example graph above. The extra points are for explaining what that Set.maxView and foldr business is about.

('a','x',"x")
('a','b',"b")
('a','d',"d")
('a','e',"e")
('x','b',"d")
('x','d',"d")
('x','e',"e")
('b','d',"d")
('b','e',"e")
('d','e',"e")

• 2024-06-24 – hashable arch native
• 2024-05-28 – cabal fields
• 2024-04-21 – A note about coercions
• 2024-04-18 – What makes a good compiler warning?
• 2024-04-12 – Core Inspection

twitter github email linkedin stackoverflow